https://www.acmicpc.net/problem/9938
9938번: 방 청소
문제 은기는 술병 N개(1부터 N까지 번호가 매겨져 있다)와 서랍 L개(1부터 L까지 번호가 매겨져 있다)를 가지고 있다. 술병은 은기의 방 바닥에 흩어져 있고, 어린이날을 맞이해 방 청소를 하려고 한다. 서랍에는 술병이 하나 들어갈 수 있다. 나중에 원하는 술을 빠르게 찾을 수 있게 하기 위해 은기는 각각의 술병이 들어갈 수 있는 서랍의 번호 Ai와 Bi를 공책에 적어 놓았다. 은기는 술병을 1번부터 N번까지 순서대로 정리할 것이고, 각각의 술병에 대
www.acmicpc.net
Disjoint Set을 이용한 문제입니다.
문제는 백준 알고리즘 사이트에서 확인하세요.
이번 문제는 이해하기가 너무 힘든 문제였습니다;;ㅋㅋ
문제 분석
술을 서랍에 보관하는 과정을 살펴봅시다!
- 서랍 Ai가 비어있다면, i번 술을 그 서랍에 보관한다.
- 서랍 Bi가 비어있다면, i번 술을 그 서랍에 보관한다.
- Ai에 들어있는 술을 다른 서랍으로 이동시킨다. 만약 그 서랍에도 이미 술이 들어있다면, 그 술을 다른 서랍으로 이동시킨다. 이런 과정을 거쳐서 빈 서랍을 하나 찾아 술을 모두 이동할 수 있는 경우에는, 술을 이동시키고 i번 술을 Ai에 보관한다. 불가능한 경우에는 다음 규칙으로 넘어간다.
- Bi에 들어있는 술을 다른 서랍으로 이동시킨다. 만약 그 서랍에도 이미 술이 들어있다면... (위와 같음)
- 1,2,3,4번 과정이 모두 불가능한 경우에는 i번 술을 그 자리에서 마셔버린다.
문제가 원하는 것 - 각각의 술에 대해서, 서랍에 보관할 수 있으면 'LADICA'를 출력하고
보관할 수 없으면 'SMECE'를 출력하시오.
이렇게 네/아니오로 판단하는 문제를 Decision Problem이라 합니다.
술병을 담을 서랍이 1개의 술병에 대해 2개씩 주어진다는게 이 문제의 힌트입니다.
해당 서랍이 다른 술병으로 차 있으면, 다른 빈 서랍에 넣는 문제인데요.
다른 빈 서랍을 어떻게 찾을까요?
문제 해결
문제의 예제를 보면서 disjoint set를 찾아볼게요~!
1 2
3 4
5 6
7 8
9 10
위의 입력은 모두 과정 1에 해당되므로 아래와 같이 표현할 수 있습니다.
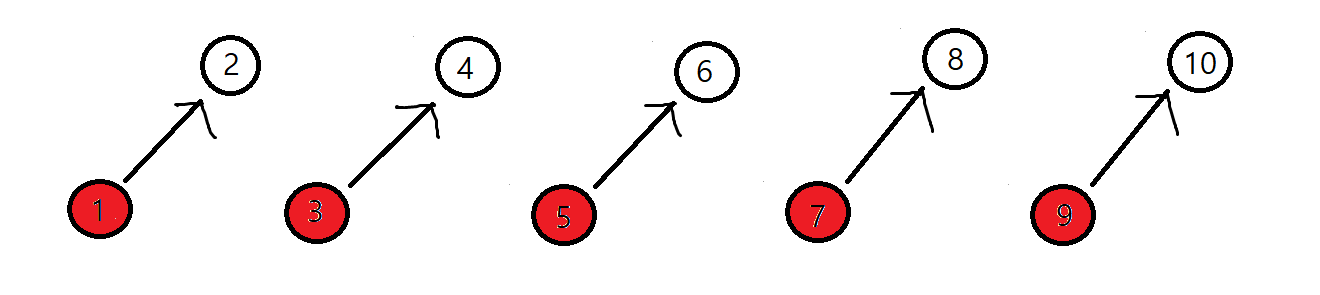
2 3

왜 2->3이 아닌 2->4를 갈까요?
disjoint set의 ADT인 find()함수는 disjoint set의 root 노드를 가리키기 때문입니다!
1 5

8 2
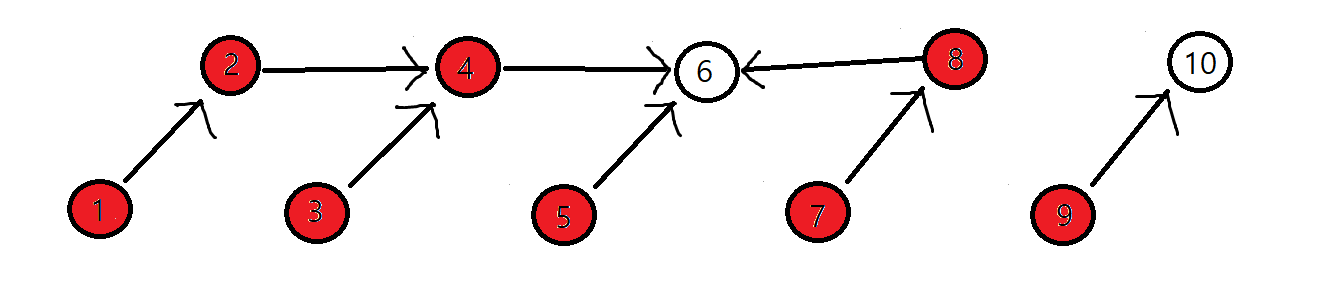
7 9
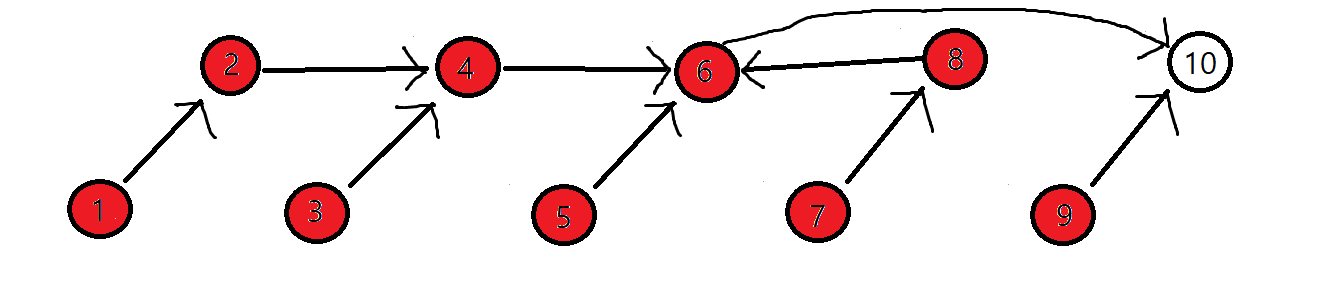
예제의 모든 입력에 대한 출력은 LADICA(보관할 수 있음)이 됩니다.
필요한건 각 집합에 대한 root 노드겠네요.
find 함수의 효율을 보다 높이기 위해 반복문이 아닌 Tail Recursion(꼬리 재귀)와 일종의 memoization을 사용한 find 함수를 사용하겠습니다~
int find(int i) {
if (parent[i]==i) {
return i;
}
else {
return parent[i] = find(parent[i]);
}
}이렇게 작성하면 같은 집합에 있는 모든 parent들은 바로 위의 parent를 가리키는 것이 아닌 root를 가리키게 됩니다.
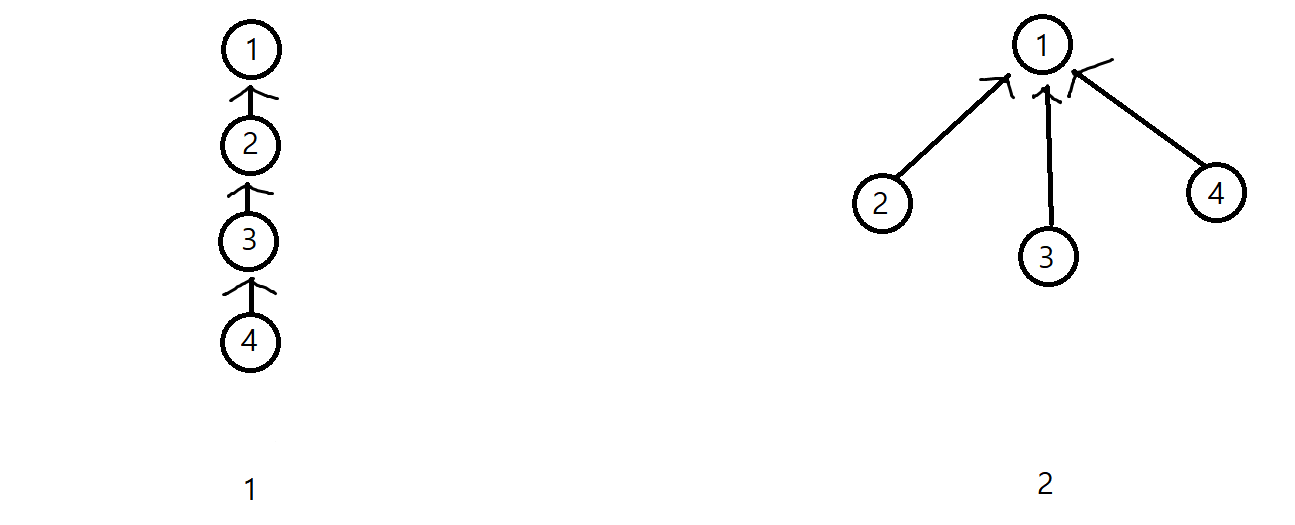
1번 방식은 4에서 root까지 가기위해 3번 find를 호출해야합니다.
2번 방식은 node 2,3,4에서 root까지 find를 한번만 호출해서 접근할 수 있습니다~
이렇게 코딩하면 중간 서랍에 빈곳이 있을때 못넣잖아요? 라는 의문이 생길 수 있는데요!
이 문제점을 해결하기 위해 각 disjoint set의 root에 빈 서랍의 수를 적어놓는 방법을 사용합니다
다음은 이 문제의 소스코드입니다.
#include <iostream>
#include <vector>
using namespace std;
int parent[300001];
int root[300001];
void merge(int a, int b);
int find(int i);
int main() {
int n, l, a, b;
ios::sync_with_stdio(false);
cin.tie(NULL);
cin >> n >> l;
for(int i=1; i<=l; i++){
parent[i] = i;
root[i] = 1;
}
for (int k = 1, ta, tb; k <= n; k++) {
cin >> a >> b;
a = find(a);
b = find(b);
if (root[a] >= 1) {
root[a]--;
merge(a, b);
root[b] += root[a];
}
else if (root[b] >= 1) {
root[b]--;
merge(b, a);
root[a] += root[b];
}
else {
printf("SMECE\n");
}
}
}
int find(int i) {
if (parent[i]==i) {
return i;
}
else {
return parent[i] = find(parent[i]);
}
}
void merge(int a, int b) {
if (find(a) != find(b)) {
parent[a] = b;
}
printf("LADICA\n");
}
'Algorithms > Baekjoon Algorithms' 카테고리의 다른 글
| 백준 알고리즘 2188번 문제 : 축사배정 (0) | 2019.08.11 |
|---|---|
| 백준 알고리즘 2512번 문제 : 예산 (0) | 2019.07.17 |
| 백준 알고리즘 2302번 문제 : 극장 좌석 (0) | 2019.07.10 |
| 백준 알고리즘 2580번 문제 : 스도쿠 (0) | 2019.07.08 |
| 백준 알고리즘 1238 - 파티 (0) | 2019.07.02 |

